こんにちは、のっくんです。
今日は主成分分析について、かなり分かりやすく説明します。
主成分分析するメリットは一言で言うと、
「次元数の削減です」
例えば、
「身長、体重、年、性別」
の4つのデータがあったとして、これを主成分分析することにより2つのデータ(主成分1と主成分2)に変換することができます。
このように4から2に次元数を削減することで、データ容量を減らせるメリットがあります。
PythonのScikitLearnでPCAのやり方を見ていきましょう。
Google Colabを使ってコードを書いていきます。
Google Colabにはsklearnなどの今回使用するライブラリが全部インストールされています。
[toc]
使用するデータ
使用するデータはこちら。
UCIのレポジトリにあるアヤメのデータセット。
本ブログでも何回か登場しています。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
%matplotlib inline
df = pd.read_csv(
filepath_or_buffer='https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data',
header=None,
sep=',')
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
花ビラの長さを含む4つの特徴から構成されています。
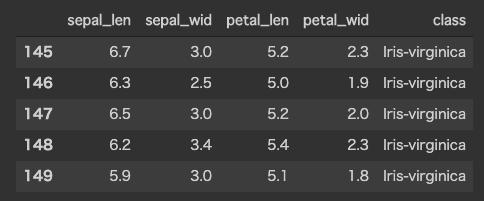
標準化と主成分分析
PCAを行う前にこの4次元のデータを標準化して、-1から1の範囲に収める必要があります。
sklearnに付属しているStandardScalarを使い標準化します。
X = df.iloc[:,0:4].values y = df.iloc[:,4].values #-1 - 1の範囲にする X_std = StandardScaler().fit_transform(X)
次にPCAで主成分分析をします。
コンポーネント数を2に指定することで、2つの主成分に分解します。
ca = PCA(n_components=2)
principalComponents = pca.fit_transform(X_std)
principalDf = pd.DataFrame(data = principalComponents
, columns = ['principal component 1', 'principal component 2'])
principalDf.head(5)
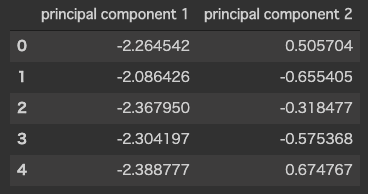
以下のコードで、この2つの主成分の分散説明率と固有ベクトルが分かります。
print("主成分の分散説明率")
print(pca.explained_variance_ratio_)
print("固有ベクトル")
print(pca.components_)
主成分の分散説明率 [0.72770452 0.23030523] 固有ベクトル [[ 0.52237162 -0.26335492 0.58125401 0.56561105] [ 0.37231836 0.92555649 0.02109478 0.06541577]]
分散説明率を足すと95%となり、元の4次元のデータの約95%の情報を2次元で保持していることが分かります。
データの2Dマッピング
主成分のデータを図にマッピングしてみます。
アヤメの種類は3種類なので、それぞれRGBで表すようにします。
finalDf = pd.concat([principalDf, df[['class']]], axis = 1)
finalDf.head(5)
fig = plt.figure(figsize = (8,5))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 Component PCA', fontsize = 20)
targets = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
indicesToKeep = finalDf['class'] == target
ax.scatter(finalDf.loc[indicesToKeep, 'principal component 1']
, finalDf.loc[indicesToKeep, 'principal component 2']
, c = color
, s = 50)
ax.legend(targets)
ax.grid()

3種類のアヤメが二次元上に分別して表示されました。
4次元のデータを2次元で表現できるってすごくないですか?
元データの95%がこの2次元の特徴で表せているんです。
主成分分析ってすげえ。
おわり。










